Non-Newtonian Generating Functions

Introduction and Preliminaries

Generating functions are one of most suprising topics in mathematics. They are used many fields of cryptograhy, mathematics, computational science and else. Non-Newonian calculus was firstly introduced by Grossman and Katz as an alternative to classical calculus[1]. It provides wide diversity of mathematical instruments which are useful in engineering, mathematics and science. Non-Newtonian calculus was used by Meginniss to create a theory of probability that is adapted to human behavior and decision making[2]. Rybaczuk and Stopel used the bigeometric calculus on fractals and material science[3]. In a study which is made by Aniszewska and Rybaczuk, the bigeometric calculus was used on a multiplicative Lorenz system[4]. In a study which is made by Bashirov and Riza, differentiation analysed as complex multiplicative[5]. The non-Newtonian calculus was used in the study of biomedical image analysis by Florack and van Assen[6]. Çakmak and Başar obtained some results and sequence spaces with respect to non-Newtonian calculus[7]. In a study which is made by Tekin and Başar, sequence spaces were examined on non-Newtonian complex field[8]. Duyar, Sagir and Oğur got some basic topologic properties on non-Newtonian real line[9]. Duyar and Erdoğan investigated non-Newtonian real number series and non-Newtonian improper integrals, and they obtained convergence tests for them[10, 11]. Sağir and Erdoğan studied non-Newtonian power series[12]. Güngör examined geometric properties of non-Newtonian sequence space l_p(N)[13].

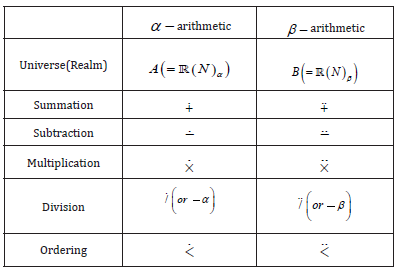
generator is one-to-one function whose domain is  , the set of all real numbers, and whose range is a subset of  . The range of generator α is called non-Newtonian real line and we denote it by (N) _α . By α − arithmetic we mean the arithmetic whose realm (N) α and whose operations and ordering relation are defined as follows:

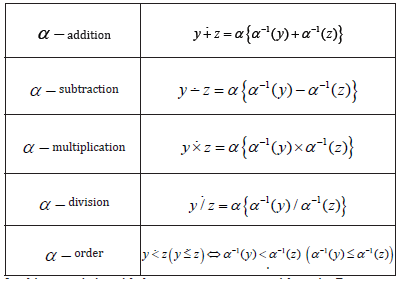
In this case, it is said that α generates α − arithmetic. For example, the identity function I generates the classical arithmetic and the exponential function exp generates geometric arithmetic. Each generator generates exactly one arithmetic and, conversely, each arithmetic is generated by exactly one generator[1].

The α − positive numbers are the numbers in (N) α such that x > 0 , similarly the α − negative numbers are the numbers in (N) α such that x < 0 . α − zero and α − one numbers are denoted by 0 =α (0) and 1 =α (1) respectively. α − integers are obtained by successive α − addition of 1 to 0 and successive α − subtraction of 1 from 0 . Hence α − integers are as follows:

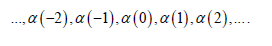
For each integer n , we set n =α (n) . If n is an α − positive integer, then it is n times α − sum of 1 [1].

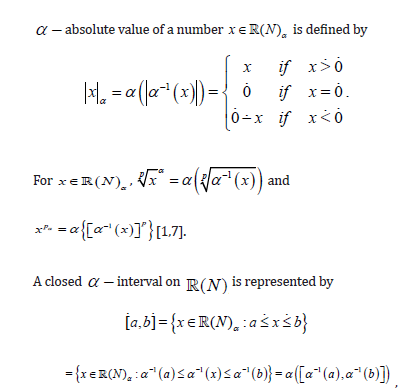
similarly an open α − interval (a,b) can be represented. It is said that an α − interval has α − extent b a − [9].

Let {u_n} be an infinite sequence of the numbers in R(N)_α . If each open α − interval containing an element u includes all ele{ men}ts except for a finite numbers of elements of the sequence {u_n} , then it is said that the sequence {u_n} α − converges to u and the element u is called as α − limit of the sequence {u_n} . This is denoted by

. This convergence becomes the classic convergence if α = I . Classic and geometric convergence are equivalent in the sense that a positive number sequence {P_n} converges as geometric to a positive number p iff { } n p converges as classic to p [1].

.

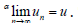
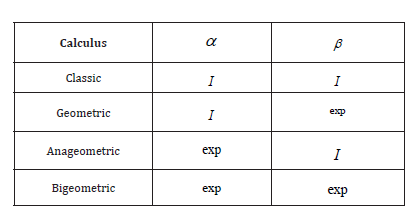
Let α and β be arbitrary chosen generators which image the set  to A and B respectively. *-Calculus is defined as an ordered pair of the arithmetics (α − arithmetic, β − arithmetic) and the following notations are used:

α − arithmetic is used on inputs and β − arithmetic is used on outputs. In particular, the changes of inputs and outputs are measured by α − arithmetic and β − arithmetic, respectively. The operators in *-calculus are applied to functions whose inputs and outputs belong to A and B , respectively [1].

If the generators α and β are chosen as one of I and exp , the following special calculuses are obtained.

The isomorphism from α − arithmetic to β − arithmetic is the unique function ι (iota) that possesses the following three properties:
• (i) ι is one to one,
• (ii) ι is on A and onto B ,
• (iii) For any number u and v in A ,

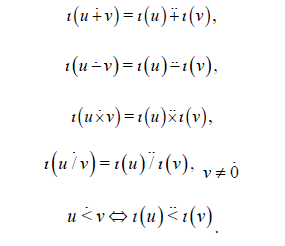
It turns out that ι ( x) = β {α ⁻¹ ( x)} for every number x in A , and that

ι (n) = n for every integer n . Any statement in α − arithmetic can easily transformed into a statement in β − arithmetic thanks to the isomorphism ι [1].

Non-Newtonian Generating Functions

Definition 4.1: Let (a_n)be a sequence in R(N)_α , namely, be an α − sequence. Then the *-power series

which has sequence coefficients (t(a_n)) is called *-generating function or non-Newtonian generating function for the sequence (a_n). Similarly, when (b_n) is a sequence in (N)_β  , namely a β − sequence, *-power series

which has sequence coefficients (b_n) is called *-generating function or non-Newtonian generating function for the sequence (b_n) n b .

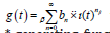
Example 4.2: Let *-generating function of constant α − sequence ( ) 1 and constant β − sequence (1) be found. Additionally let these *-generating functions be examined in geometric, anageometric and bigeometric calculus.

Solution 4.3: The *-generating function of constant α − sequence ( ) 1 is the *-power series

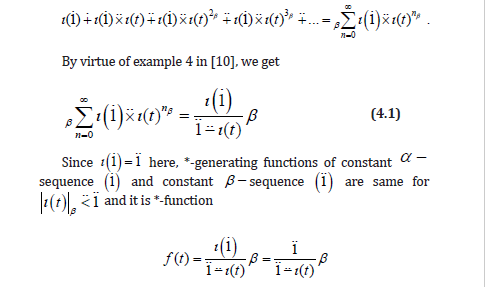
As in classical generating functions, we don’t consider *-convergence intervals of *-generating functions and we consider that they are *-convergent. Now, let these sequence and functions be examined for special calculus. Since α = I , β = exp for geometric calculus, constant α − sequence ( ) 1 is constant sequence (1) and *-generating function is

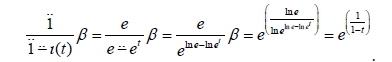
From here, it is seen that *-generating functions of constant sequence (1) in geometric calculus is e^(1/1-t). It is well known that generating function of constant sequence (1) in classical calculus is the function 1/1− t . This shows us that generating functions of same sequence can be different in different calculus.

Since α = exp , β = I for anageometric calculus, constant α − sequence ( ) 1 is constant sequence (e) and *-generating function is

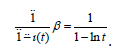
It is easily seen that generating function of constant sequence (e) in classical calculus is e/1− t . This shows us that generating functions of same sequence can be different in different calculus.

Since α = β = exp for bigeometric calculus, constant α − sequence ( ) 1 is the constant sequence (e) and *-generating function is

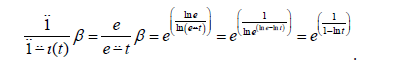
Again, this shows us that generating functions of same sequence can be different in different calculus.

Example 4.4: Find that *-generating function and general term of sequence (a_n) which holds recurrence a_n+1=(3×a_n)+2 for n ≥ 0 and a₀ = 0 .

Solution 4.5: Primarily, let’s take image of each side of recurrence under ι.

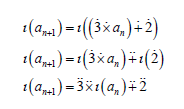
If each side of equality above be β − multiplicated by t(t)^nβ and be β − summed for n ≥ 0 , then

If equality be β −multiplicated by ι (t) in order to make left hand sum similar to the function A(t ) ,

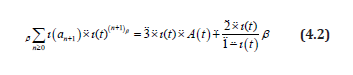
is obtained. Here, only difference of β − series at left side of 2.2 from A(t ) is that there is no term ι(a₀) in β − sum. Hence left side is A_ι A₀ −ι(a₀) . ι(a₀) = 0 since a₀ = 0 , thus left side is found as A(t ) − 0 = A(t ) . If we substitute this in 2.2, then we find *-generating function of (a_n) as

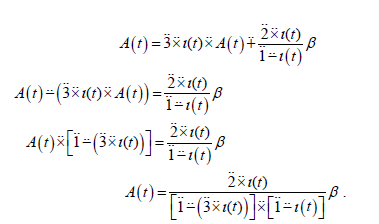
Now, we must expand the *-generating function A(t ) in partial fractions to find general term of the sequence (a_n). Therefore, let .

is written. When this well known operation of expanding in partial fractions is completed, it is found that β ⁻¹ (m) =1 and β −1 (k ) = −1. Hence m = 1 and k = 0 −1. From here,

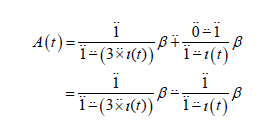
is obtained. In view of *-generating function 2.1, if we expand the *-generating function A(t ) in *-power series, we get

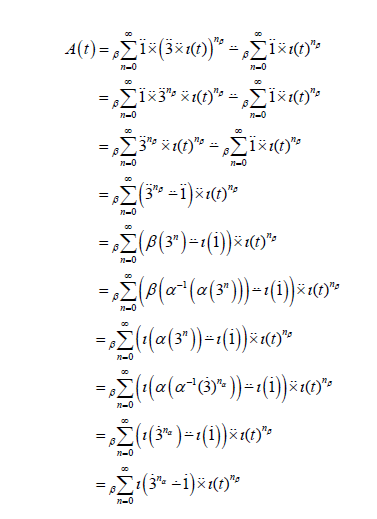
Therefore 3n 1 n a =  α −  is obtained.

Example 4.6: Find that *-generating function for sequence a_n with n ≥1 and

in geometric calculus.

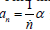
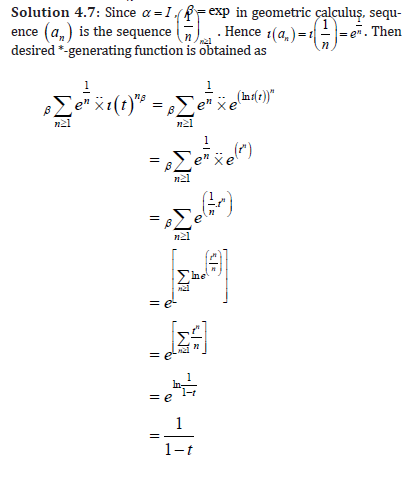
Definition 4.10: A *-formal power series is an expression of the form

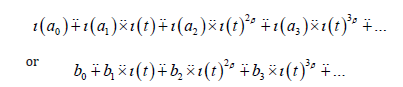
where the α − sequence (a_n) and the β − sequence (b_n) are called sequence of coefficients.

To say that two *-formal power series are equal is to say that coefficient sequences are the same. Since the function ı is an isomorphism from α − arithmetic to β − arithmetic, (ι(a_n)) is a β − sequence for given α − sequence (a_n) and ( ι^-1(b_n)) is an α − sequence for given β − sequence (b_n) . Due to this situation, features for *-formal power series will be shown over only α − sequences or only β − sequences. By virtue of the function ı, having a feature in one will require it to have in the other.

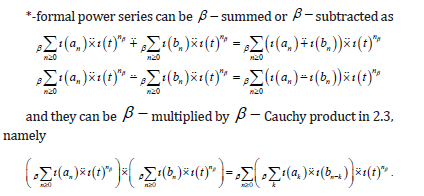
One can easily see that *-formal power series forms a ring with operations mentioned above.

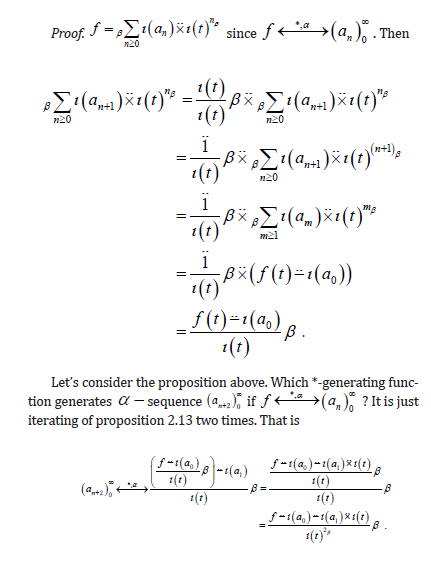
In this way, general case of proposition 2.13 is given below. One can easily prove that by induction.

Acknowledgement

None.

Conflict of Interest

No conflict of interest.

References

1. Grossman M, Katz R (1972) Non-Newtonian Calculus, Lee Press, Pigeon Cove, Massachusetts.
2. Meginniss J R (1980) Non-Newtonian calculus applied to probability, utility, and Bayesian Analysis. American Statistical Assoiation: Proceedings of the Business and Economic Statistics Section, 405-410.
3. Rybaczuk M, Stoppel S (2000) The fractal growth of fatigue defects in materials. Springer 103(1): 71-94.
4. Aniszewska D, Rybaczuk M (2005) Analysis of the multiplicative Lorenz system. Chaos, Solitons and Fractals 25(1): 79-90.
5. Bashirov A E, Riza M (2011) On complex multiplicative differentiation. TWMS Journal of Applied and Engineering Mathematics 1(1): 75-85.
6. Florack L, Van Assen H (2012) Multiplicative calculus in biomedical image analysis. Journal of Mathematical Imaging and Vision 42(1): 64-75.
7. Cakmak A F, Başar F (2012) Some new results on sequence spaces with respect to non-Newtonian calculus. Journal of Inequalities and Applications 228(1): 1-17.
8. Tekin S, Başar F (2013) Certain sequence spaces over the non-Newtonian complex field. Abstract and Apllied Analysis 2013: 1-11.
9. Duyar C, Sagir B, Ogur O (2015) Some basic topological properties on non-newtonian real line. British Journal of Mathematics & Computer Science 9(4): 300-307.
10. Duyar C, Erdogan M (2016) On non-Newtonian real number series. IOSR Journal of Mathematics 12(6): 34-48.
11. Duyar C, Erdogan M (2018) Non-Newtonian Improper Integrals. Journal of Science and Arts 1(42): 49-78.
12. Sağır B, Erdoğan F (2020) On Non-Newtonian Power Series and Its Applications. Konuralp Journal of Mathematics 8(2): 294-303.
13. Güngör N (2020) Some geometric properties of the non-Newtonian sequence spaces lp(N). Mathematica Slovaca 70(3): 689-696.